Generating The Fibonacci Sequence in C#

Content

Introduction

We will look at possible solutions for generating the Fibonacci sequence in C#.

Fibonacci is a number sequence that starts with 0, 1, 1 and then the following number is the addition of the two preceding numbers:

We will also look into the yield keyword and how to use it to generate the Fibonacci sequence.

You will see how you can use the most popular benchmarking library, BenchmarkDotNet, to observe the performance of a given solution and compare it to other solutions.

All solutions can be found on the following GitHub repository. I have been using Visual Studio 2022, but in general, you should be able also to use any .NET C# IDE of your choice.

matthiasjost/FibonacciSequence

I encourage you to develop your solutions and challenge the ones I listed here. The goal is to play with the different mechanics C# offers you to find other solutions to this problem.

Solution 1: List and For-Loops (Index)

The solution is just two nested for-loops, where the outer loop iterates until the desired sequenceLength is reached. The inner loop iterates backwards, starting at the current index (index) and ending at the index that is two places before it. This adds the last two numbers in the list together and stores the result in the next variable.

[Benchmark(Baseline = true)]
public List<BigInteger> Generate1() => Generate1(SequenceLength);
public List<BigInteger> Generate1(int sequenceLength)
{
    List<BigInteger> fibonacci = new List<BigInteger>();
    fibonacci.Add(0);
    fibonacci.Add(1);
    BigInteger next = 0;
    for (int index = 1; index < sequenceLength; index++)
    {
        next = 0;
        for (int i = index; i > index - 2; i--)
        {
            next += fibonacci[i];
        }
        fibonacci.Add(next);
    }
    return fibonacci;
}

Solution 2: List and For-Loops (list.Count)

The second solution only differs in terms of its inner loop. list.Count is used.

[Benchmark]
public List<BigInteger> Generate2() => Generate2(SequenceLength);
public List<BigInteger> Generate2(int sequenceLength)
{
    List<BigInteger> fibonacci = new List<BigInteger>();
    fibonacci.Add(0);
    fibonacci.Add(1);
    BigInteger next = 0;
    for (int index = 1; index < sequenceLength; index++)
    {
        next = 0;
        for (int i = fibonacci.Count - 1; i > fibonacci.Count - 3; i--)
        {
            next += fibonacci[i];
        }
        fibonacci.Add(next);
    }
    return fibonacci;
}

Solution 3: Using LINQ Skip and Reverse Methods

The third solution makes use of the Reverse() and Skip() Methods.
The idea is to reverse the list and skip the first or second item.

[Benchmark]
public List<BigInteger> Generate3() => Generate3(SequenceLength);
public List<BigInteger> Generate3(int sequenceLength)
{
    List<BigInteger> fibonacci = new List<BigInteger>();
    fibonacci.Add(0);
    fibonacci.Add(1);
    BigInteger next = 0;
    for (int index = 1; index < sequenceLength; index++)
    {
        next = 0;
        IEnumerable<BigInteger> reversedList = fibonacci.AsEnumerable().Reverse();
        next += reversedList.Skip(0).First();
        next += reversedList.Skip(1).First();
        fibonacci.Add(next);
    }
    return fibonacci;
}

Solution 4: Using LINQ Skip

Solution 4 is slightly different. It doesn’t reverse the list. Instead, it uses the list.Count to skip the desired number of items.

[Benchmark]
public List<BigInteger> Generate4() => Generate4(SequenceLength);
public List<BigInteger> Generate4(int sequenceLength)
{
    List<BigInteger> fibonacci = new List<BigInteger>();
    fibonacci.Add(0);
    fibonacci.Add(1);
    BigInteger next = 0;
    for (int index = 1; index < sequenceLength; index++)
    {
        next = 0;
        next += fibonacci.Skip(fibonacci.Count - 1).First();
        next += fibonacci.Skip(fibonacci.Count - 2).First();
        fibonacci.Add(next);
    }
    return fibonacci;
}
ist;
}

Solution 5: Using LINQ Skip Again

Solution 5 is almost the same as four. It reduced the number of variables but made the code a bit harder to read.

[Benchmark]
public List<BigInteger> Generate5() => Generate5(SequenceLength);
public List<BigInteger> Generate5(int sequenceLength)
{
    List<BigInteger> fibonacci = new List<BigInteger>();
    fibonacci.Add(0);
    fibonacci.Add(1);
    while (fibonacci.Count < sequenceLength)
    {
        fibonacci.Add(fibonacci.Skip(fibonacci.Count - 2).First()
                 + fibonacci.Skip(fibonacci.Count - 1).First());
    }
    return fibonacci;
}

Solution 6: Trying Something Different – Yield (1)

Using yield feels like magic if it is not yet part of your toolbox.

In the example provided, the Generate6 method is an iterator method that returns an IEnumerable<int>. It uses the yield return statement to yield a sequence of integers to the caller.

public IEnumerable<BigInteger> Generate6Yield()
{
    BigInteger first = 0;
    BigInteger second = 1;
    yield return first;
    yield return second;
    while (true)
    {
        BigInteger temp = first;
        first = second;
        second = second + temp;
        yield return second;
    }
}

[Benchmark]
public List<BigInteger> Generate6YieldToList() => Generate6Yield(SequenceLength);
public List<BigInteger> Generate6Yield(int sequenceLength)
{
    int index = 0;
    List<BigInteger> fibonacci = new List<BigInteger>();
    foreach (var generate in Generate6Yield())
    {
        fibonacci.Add(generate);
        index++;
        if (index == sequenceLength)
        {
            break;
        }
    }
    return fibonacci;
}

As you see, Generate6Yield is called directly from within the foreach loop to get the following Fibonacci number.

What You Should Know About Yield

Most things we saw before are probably already in your muscle memory, or you intuitively get what it does. Regarding the yield keyword, it makes sense to develop a mental model despite its use not being as intuitive as the other presented solutions.

IEnumerable and IEnumerator Interfaces

yield is used either with IEnumerable or IEnumerate to implement so-called iterator methods.

To have a mental model of how it works when using yield. You may think of it as being just streaming.

Let us have a look at all relevant interfaces:

public interface IEnumerable<out T> : IEnumerable
{
    new IEnumerator<T> GetEnumerator();
}

IEnumerable<out T> inherits from IEnumerable

public interface IEnumerable
{
    IEnumerator GetEnumerator();
}

So both interfaces depend on IEnumerator, It’s time to look at that interface as well!

public interface IEnumerator
{
    bool MoveNext();
    void Reset();
}

I removed some of the code and comments from the interfaces that do not help explain the case. If you want to see the complete code, just hit “Go to definition” from within Visual Studio or the IDE of your choice.

The key takeaways when looking at those interfaces are the following:

Everyone implementing an iterator method with the help of IEnumerable and, therefore also, IEnumerator must implement the MoveNext() method and, therefore, cannot be stateless but rather hold its internal state respectively position in this “streamed” list.
yield adds the syntactic sugar to hide that state machine from you, so to say, another abstraction to your code that makes it shorter and boils it down to something elegant.

Also, it is worth pointing out the close relationship between foreach and yield.

Essentially, both concepts hide some of the complexity that can be seen again when we know what the compiler does behind the scenes with your foreach iterator method.

In terms of a foreach loop: This is not exactly what the compiler does, but it’s instead an example of what the code might look like if it compiles:

IEnumerator<int> enumerator = collection.GetEnumerator();
while (enumerator.MoveNext())
{
    // do something within each iteration
}

Why Yield?

Why should I care about it when it’s less intuitive and more complex to read than other techniques?

The answer probably doesn’t surprise you: It is another tool in your toolbox. The more tools you know, the better.

A Picture Says More Than…

A picture says more than thousands of words. So here is an illustration of how you can think of a traditional method of aggregating a list of payload items and returning it:

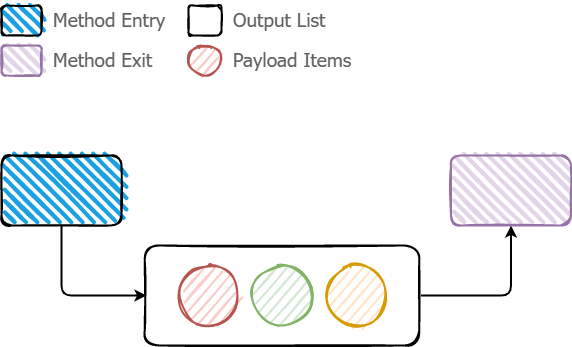
As you can see in the illustration. The whole list is generated during that single method call, and the items are added to a List.

Here, we see what it looks like when streaming the data with yield:

There is no need for a List. The method gets called every time the caller wants a new item. The data is streamed and not aggregated as a list.

Solution 7: Trying Something Different – Yield (2)

Just a change to the calling method of solution 6 to try to make the code faster:

[Benchmark]
public List<BigInteger> Generat7YieldTake() => Generate7Yield(SequenceLength);
public List<BigInteger> Generate7Yield(int sequenceLength)
{
    List<BigInteger> fibonacci = new List<BigInteger>();
    fibonacci = Generate6Yield().Take(sequenceLength).ToList();
    return fibonacci;
}

Solution 8: Array List

An array list is an array that can hold any object as an item. You can also say it is not statically typed. Therefore, you must “unbox” the value to the correct data type.

[Benchmark]
public ArrayList Generate8() => Generate8(SequenceLength);
public ArrayList Generate8(int sequenceLength)
{
    ArrayList fibonacci = new ArrayList();
    fibonacci.Add((BigInteger)0);
    fibonacci.Add((BigInteger)1);
    BigInteger next = 0;
    for (int index = 1; index < sequenceLength; index++)
    {
        next = 0;
        for (int i = index; i > index - 2; i--)
        {
            next = (BigInteger)fibonacci[i] + next;
        }
        fibonacci.Add(next);
    }
    return fibonacci;
}

The value in this example gets unboxed, which means it gets copied from a reference of the hap onto a value type of the stack. This is not beneficial to our performance, as we can see later in the results.

Please note that ArrayList was introduced before there existed generic Lists. Generic lists are better because they do not involve boxing and unboxing, which adds overhead (e.g. List<T>) when accessing an item on the list.

Solution 9: Array

The array is the most straightforward solution I can think of. You define an array whose size is known during compile time (SequenceLength is a variable that is defined as const on the class level).

[Benchmark]
public BigInteger[] Generate9() => Generate9(SequenceLength);
public BigInteger[] Generate9(int sequenceLength)
{
    BigInteger[] fibonacci = new BigInteger[sequenceLength];
    fibonacci[0] = 0;
    fibonacci[1] = 1;
    BigInteger next = 0;
    for (int index = 2; index < sequenceLength; index++)
    {
        next = 0;
        for (int i = index; i > index - 3; i--)
        {
            next += fibonacci[i];
        }
        fibonacci[index] = next;
    }
    return fibonacci;
}

Solution 10: Array With Span<>

Span is a way to address consecutive memory. For an in-depth overview of the Span keyword, I recommend an article on the ndepend blog: Improve C# code performance with Span<T>.

[Benchmark]
public Span<BigInteger> Generate10() => Generate10(SequenceLength);
public Span<BigInteger> Generate10(int sequenceLength)
{
    Span<BigInteger> fibonacci = new Span<BigInteger>(new BigInteger[sequenceLength]);
    fibonacci[0] = 0;
    fibonacci[1] = 1;
    BigInteger next = 0;
    for (int index = 2; index < sequenceLength; index++)
    {
        next = 0;
        for (int i = index; i > index - 3; i--)
        {
            next += fibonacci[i];
        }
        fibonacci[index] = next;
    }
    return fibonacci;
}

Solution 11: Array Without Helper Variable

The following code eliminates the need for the next helper variable:

[Benchmark]
public BigInteger[] Generate11() => Generate11(SequenceLength);
public BigInteger[] Generate11(int sequenceLength)
{
    BigInteger[] fibonacci = new BigInteger[sequenceLength];
    fibonacci[0] = 0;
    fibonacci[1] = 1;
    for (int index = 2; index < sequenceLength; index++)
    {
        fibonacci[index] = fibonacci[index - 2] + fibonacci[index - 1];
    }
    return fibonacci;
}

Measuring Performance With BenchmarkDotNet

Suppose you want to know how to set up a solution with BenchmarkDotNet. In that case, I recommend you clone the repository (matthiasjost/FibonacciSequence) that belongs to this article.

I will quickly summarize the key takeaways with the related code snippets here. This is not a step-by-step guide but an overview. I recommend reading A Step by Step Guide to Benchmarking in .NET by Philippe Vaillancourt to learn how to have it in your solution step by step.

Also, don’t forget to look at the official BenchmarkDotNet Homepage: benchmarkdotnet.org

Where Are The Relevant Source Code Parts To Execute And Configure BenchmarkDotNet

A .NET Console application with a unique “startup” code is required to run your benchmarks:

var summary = BenchmarkRunner.Run<FibonacciGenerator>();
System.Console.ReadLine();

FibonacciGenertor is the class that is instantiated to run the benchmark.

Every method that has the Benchmark decorator will get executed during the benchmark.

 [Benchmark]

Also, you can set the baseline:

[Benchmark(Baseline = true)]

The baseline defines which method will be defined with a ratio of 1.00 whereas other methods get their respective factor depending on their execution time.

BenchmarkDotNet is going to show you a table in the console with these columns:

Mean: Arithmetic mean of all measurements
Error: Half of 99.9% confidence interval
StdDev: Standard deviation of all measurements

Executing The Benchmark

Build the Release version of the console project. An attached debugger might affect your results!
Then, execute the executable from Windows Explorer or your Console.

You will notice a lot of output in the console window.

For every benchmark execution, a version of your benchmark gets built and automatically created in the \bin\Release\net.6.0\ folder of your benchmark project. See this example output:

// Validating benchmarks:
// ***** BenchmarkRunner: Start   *****
// ***** Found 9 benchmark(s) in total *****
// ***** Building 1 exe(s) in Parallel: Start   *****
// start dotnet  restore /p:UseSharedCompilation=false /p:BuildInParallel=false /m:1 /p:Deterministic=true /p:Optimize=true in C:\Users\matth\Documents\GitHub\FibonacciSequence\FibonacciSequence.Console\bin\Release\net6.0\4a3d4a00-66fd-432f-97de-3fb961a6d81b
// command took 0.9s and exited with 0
// start dotnet  build -c Release --no-restore /p:UseSharedCompilation=false /p:BuildInParallel=false /m:1 /p:Deterministic=true /p:Optimize=true in C:\Users\matth\Documents\GitHub\FibonacciSequence\FibonacciSequence.Console\bin\Release\net6.0\4a3d4a00-66fd-432f-97de-3fb961a6d81b
// command took 1.88s and exited with 0
// ***** Done, took 00:00:02 (2.87 sec)   *****
// Found 9 benchmarks:
//   FibonacciGenerator.Generate9: DefaultJob
//   FibonacciGenerator.Generate8: DefaultJob
//   FibonacciGenerator.Generat7YieldTake: DefaultJob
//   FibonacciGenerator.Generate6YieldToList: DefaultJob
//   FibonacciGenerator.Generate5: DefaultJob
//   FibonacciGenerator.Generate4: DefaultJob
//   FibonacciGenerator.Generate3: DefaultJob
//   FibonacciGenerator.Generate2: DefaultJob
//   FibonacciGenerator.Generate1: DefaultJob

The benchmark will start in a particular way: In its default configuration, your code will not run once but multiple times. You will also notice some output during this phase:

OverheadJitting  1: 1 op, 274900.00 ns, 274.9000 us/op
WorkloadJitting  1: 1 op, 404100.00 ns, 404.1000 us/op

OverheadJitting  2: 16 op, 458000.00 ns, 28.6250 us/op
WorkloadJitting  2: 16 op, 851000.00 ns, 53.1875 us/op

WorkloadPilot    1: 16 op, 290500.00 ns, 18.1562 us/op
[...]


OverheadWarmup   1: 32768 op, 107300.00 ns, 3.2745 ns/op
[...]


OverheadActual   1: 32768 op, 121400.00 ns, 3.7048 ns/op
[...]


WorkloadWarmup   1: 32768 op, 597844300.00 ns, 18.2448 us/op
[...]

// BeforeActualRun
WorkloadActual   1: 32768 op, 591416200.00 ns, 18.0486 us/op
[...]

// AfterActualRun
WorkloadResult   1: 32768 op, 591297400.00 ns, 18.0450 us/op
WorkloadResult   2: 32768 op, 589248900.00 ns, 17.9824 us/op

BenchmarkDotNet executes the benchmark multiple times. What you will find interesting is what it takes to have a reliable benchmark; I am going to quote the GitHub Readme:

“A lot of hand-written benchmarks produce wrong numbers that lead to incorrect business decisions. BenchmarkDotNet protects you from most of the benchmarking pitfalls and allows achieving high measurement precision.

You shouldn’t worry about the perfect number of method invocation, the number of warm-up and actual iterations: BenchmarkDotNet tries to choose the best benchmarking parameters and achieve a good trade-off between the measurement prevision and the total duration of all benchmark runs. So, you shouldn’t use any magic numbers (like “We should perform 100 iterations here”), the library will do it for you based on the values of statistical metrics.

BenchmarkDotNet also prevents benchmarking of non-optimized assemblies that was built using DEBUG mode because the corresponding results will be unreliable. It will print a warning you if you have an attached debugger, if you use hypervisor (HyperV, VMware, VirtualBox), or if you have any other problems with the current environment.

During 6+ years of development, we faced dozens of different problems that may spoil your measurements. Inside BenchmarkDotNet, there are a lot of heuristics, checks, hacks, and tricks that help you to increase the reliability of the results.
BenchmarkDotNet GitHub Readme

So, there is more to benchmarking than just starting a timer to summarize this.

My Results

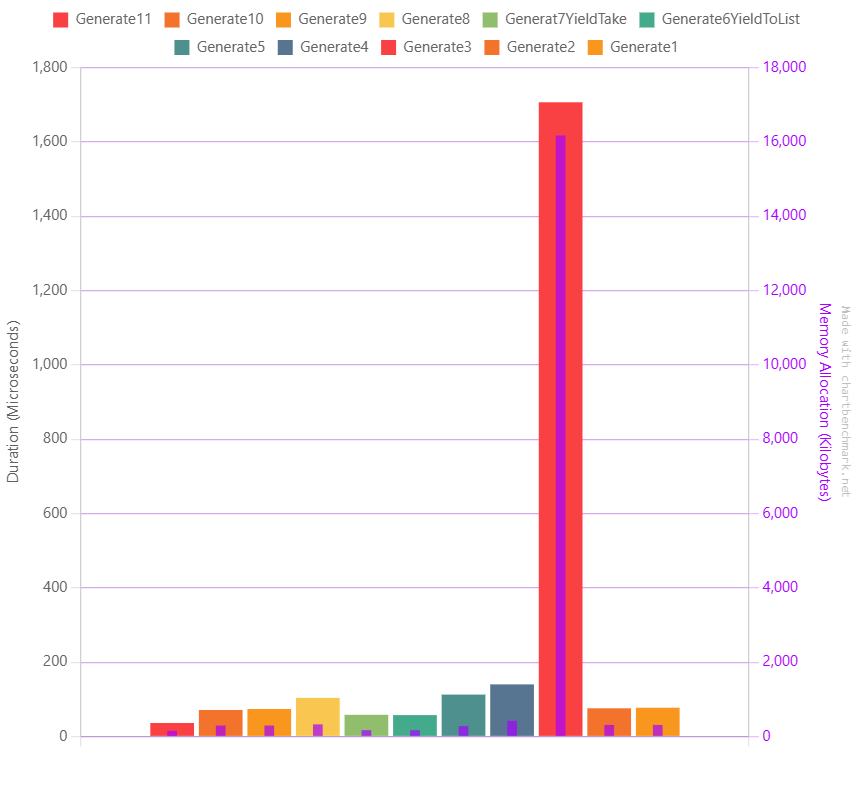
This is the result table of the console application output:

|               Method |        Mean |     Error |     StdDev | Ratio | RatioSD |      Gen0 |    Gen1 |   Allocated | Alloc Ratio |
|--------------------- |------------:|----------:|-----------:|------:|--------:|----------:|--------:|------------:|------------:|
|           Generate11 |    36.28 us |  0.629 us |   0.588 us |  0.44 |    0.03 |   25.1465 |  8.3618 |    154.1 KB |        0.50 |
|           Generate10 |    71.36 us |  0.926 us |   0.866 us |  0.86 |    0.05 |   47.9736 | 15.9912 |   293.96 KB |        0.95 |
|            Generate9 |    73.99 us |  1.410 us |   2.433 us |  0.97 |    0.10 |   47.9736 | 15.9912 |   293.96 KB |        0.95 |
|            Generate8 |   103.92 us |  4.390 us |  12.875 us |  1.35 |    0.20 |   53.2227 |  0.2441 |   326.26 KB |        1.05 |
|    Generat7YieldTake |    58.32 us |  1.988 us |   5.736 us |  0.76 |    0.12 |   27.8320 |  9.2773 |    170.8 KB |        0.55 |
| Generate6YieldToList |    57.51 us |  2.058 us |   6.068 us |  0.75 |    0.08 |   27.8320 |  9.2773 |    170.7 KB |        0.55 |
|            Generate5 |   112.74 us |  3.822 us |  11.150 us |  1.47 |    0.18 |   45.6543 | 15.1367 |   279.79 KB |        0.90 |
|            Generate4 |   140.18 us |  5.604 us |  16.435 us |  1.83 |    0.27 |   68.3594 | 22.7051 |   420.21 KB |        1.35 |
|            Generate3 | 1,706.39 us | 70.512 us | 202.312 us | 22.24 |    3.23 | 2632.8125 |  3.9063 | 16170.07 KB |       52.00 |
|            Generate2 |    75.89 us |  2.054 us |   5.958 us |  0.99 |    0.13 |   50.6592 | 16.8457 |   310.95 KB |        1.00 |
|            Generate1 |    77.40 us |  2.355 us |   6.943 us |  1.00 |    0.00 |   50.6592 | 16.8457 |   310.95 KB |        1.00 |

The following table focuses on the ratio of the different solutions and highlights the differences between the solutions:

Ratio	Description
1.00	Generate1: List and For-Loops This is our baseline. We use a list that is nothing too complicated.
0.99	Generate2: List and For-Loops `list.Count` instead of the index makes the difference here.
22.24	Generate3: Using LINQ Skip and Reverse Methods This is by far the slowest solution. We use LINQ `Skip()` and `Reverse()`. But both get called two times within a loop!
1.83	Generate4: Using LINQ Skip
1.47	Generate5: Using LINQ Skip Again Also, this solution is a lot slower than our baseline.
0.75	Generate6: Trying Something Different – Yield (1) Yield does show some fast behaviour here.
0.76	Generate7: Trying Something Different – Yield (2) Similar to the previous solution.
1.35	Generate8: ArrayList ArrayList is four times slower than our baseline the way we use it here.
0.97	Generate9: Array
0.86	Generate10: Array With Span<>
0.44	Generate11: Array without helper variable Our fastest candidate so far!

Depending on your environment, you will likely have different mean results and ratios.

You can also go to Charts for BenchmarkDotNet (chartbenchmark.net) and paste the result table from your console there to get a visualisation of your results:

A Few Words About Integers

As you have noticed, we have been using BigInteger in all the examples. We do this because a regular int wouldn’t be large enough, and your additions would lead to an overflow. In most cases, you wouldn’t even notice when you only write unit tests against a few low numbers.
You can use the checked keyword to ensure an integer does not overflow, and if it does, an exception is thrown. See also the docs: checked and unchecked statements

To get a sense of how large the Fibonacci number is when the sequence length is 1000 (which we used for our benchmarks). Here it is (209 digits):

26863810024485359386146727202142923967616609318986952340123175997617981700247881689338369654483356564191827856161443356312976673642210350324634850410377680367334151172899169723197082763985615764450078474174626

Please note you shouldn’t be using BigInteger but int in most cases. BigIntegers can hold arbitrarily large numbers but will significantly negatively impact the performance.

Feel free to lower the sequence length to speed up the total benchmark duration.

Conclusion

We saw different solutions for generating the Fibonacci number sequence in C#. Then we learned about the yield keyword and how to use it. Finally, we used the BenchmarkDotNet library to compare the solutions.

Does any of the results surprise you?

Have you found a faster solution to this problem?

Let me know!